Como calcular área de diversas formas geométricas
Compreender a definição de área é fundamental em várias áreas da matemática, física e engenharia. A área é definida como a medida de uma superfície plana, geralmente medida em unidades quadradas.
Por causa de sua importância, é essencial entender as unidades de medida da área. A unidade básica de medida de área é o metro quadrado (m²), que representa a área de um quadrado com um metro de comprimento em cada lado. No entanto, existem outras unidades de medida de área, como o centímetro quadrado (cm²) e o quilômetro quadrado (km²), que são usados para medir áreas menores e maiores, respetivamente.
Contudo, o cálculo de áreas não se limita apenas a formas regulares. Existem fórmulas específicas para calcular a área de figuras irregulares, como o trapézio e o círculo. Além disso, o cálculo de áreas é fundamental para a resolução de problemas práticos, como o cálculo de área de terrenos, pintura de paredes, entre outros.
Em suma, a compreensão do conceito de área e seu cálculo é fundamental em várias áreas da matemática, física e engenharia. O uso adequado das unidades de medida da área é fundamental para evitar erros de cálculo e garantir a precisão dos resultados.
Entendendo os fundamentos do cálculo de área:
Cálculo de áreas de Polígonos Regulares (quadrado, retângulo, triângulo)
Ao calcular a área de polígonos regulares, é importante lembrar que cada forma geométrica possui sua própria fórmula.
Apesar de cada polígono ter sua própria fórmula, há algumas informações comuns a todas as formas. Por exemplo, para calcular a área é necessário medir (com a mesma unidade métrica) as dimensões da figura.
No caso de polígonos regulares, todas as medidas dos lados e ângulos internos são iguais. Isso torna o cálculo da área ainda mais simples, uma vez que não é preciso fazer contas complicadas envolvendo medidas diferentes.
Exemplos de polígonos regulares e como calcular suas áreas
Para ilustrar, vamos dar alguns exemplos de polígonos regulares e como calcular suas áreas.
Quadrado:
Um quadrado é um polígono regular de quatro lados iguais e quatro ângulos retos. Para calcular sua área, basta elevar a medida do lado ao quadrado. Por exemplo, se o lado do quadrado mede 5 cm, a área é de 25 cm².
Quadrado: Área = lado²
Retângulo:
Um retângulo é um polígono regular de quatro lados e ângulos opostos iguais. Para calcular a área de um retângulo, basta multiplicar a medida da base pela altura. Por exemplo, se a base do retângulo mede 6 cm e a altura 4 cm, a área é de 24 cm².
Retângulo: Área = base x altura
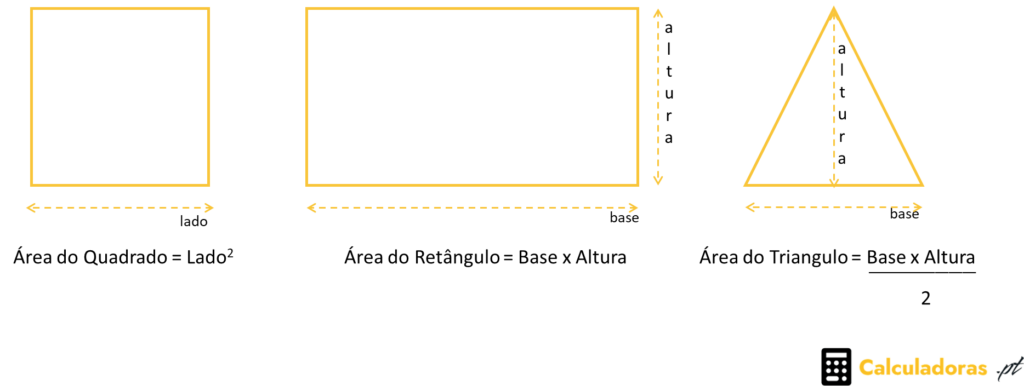
Triângulo:
Um triângulo é um polígono regular de três lados e três ângulos internos que somam 180 graus. Para calcular a área de um triângulo, basta multiplicar a base pela altura e dividir o resultado por dois. Por exemplo, se a base do triângulo mede 10 cm e a altura 6 cm, a área é de 30 cm². A dificuldade no triangulo é descobrir o valor da altura, para isso poderemos usar o Teorema de Pitágoras.
Triângulo: Área = (base x altura) / 2
Cálculo de áreas de Polígonos Irregulares
O cálculo de áreas de polígonos irregulares pode apresentar algumas dificuldades. A principal delas é que não existe uma fórmula única para calcular a área de todos os tipos de polígonos irregulares, uma vez que eles podem ter lados e ângulos de tamanhos diferentes e formas diversas.
Exemplos de polígonos irregulares e como calcular suas áreas
Um exemplo de polígono irregular comum é o pentágono irregular, que possui lados de tamanhos diferentes e ângulos internos distintos. Para calcular sua área, podemos dividi-lo em três triângulos e somar suas áreas.
Outro exemplo é a área do trapézio a qual para se obter deve-se utilizar a sua fórmula.
Técnica para medir a área de polígonos irregulares
Ao calcular a área de um polígono irregular, é necessário aplicar algumas técnicas específicas para obter um resultado preciso. Neste texto, serão apresentadas algumas dessas técnicas que podem ser utilizadas para medir a área de polígonos irregulares.
A técnica mais comum e “manual”, é a subdivisão do polígono em formas mais simples, como triângulos, retângulos ou trapézios. Em seguida, pode-se calcular a área de cada uma dessas formas simples e somá-las para obter a área total do polígono irregular. Essa técnica pode ser aplicada a polígonos com qualquer número de lados, e é uma das mais utilizadas para cálculo de áreas. Essa técnica é conhecida como decomposição em figuras planas.

Contudo, para polígonos irregulares com muitos lados, esta técnica pode tornar se bastante trabalhosa, por isso existem outras técnicas como a utilização de coordenadas cartesianas ou a utilizando software de desenho gráfico.
Cálculo de áreas de sólidos geométricos (cubo, paralelepípedo, cilindro, esfera)
Não confundir área de um sólido com o seu volume
Muitas vezes, estudantes de matemática acabam confundindo conceitos importantes na hora de calcular medidas de sólidos geométricos. Duas das grandezas mais importantes para se calcular em um sólido são a sua área e o seu volume. Porém, esses conceitos não devem ser confundidos, pois tratam de grandezas diferentes e têm aplicações distintas.
A área de um sólido é uma medida bidimensional, que se refere à extensão da superfície do objeto. Já o volume de um sólido é uma medida tridimensional, que se refere ao espaço interno do objeto. Por isso, é importante lembrar que a área de um sólido não indica a quantidade de espaço que ele ocupa, enquanto o volume indica exatamente isso.
Por causa de todas essas diferenças, é importante ter cuidado na hora de utilizar as fórmulas para calcular a área ou o volume de um sólido.
Exemplos de geométricos sólidos e como calcular suas áreas
Ao estudar geometria, é comum aprender sobre as formas planas como triângulos, quadrados e círculos. No entanto, existem também os sólidos geométricos, que são formas tridimensionais que ocupam espaço. Neste texto, vamos explorar alguns exemplos de sólidos geométricos e aprender como calcular suas áreas.
O cubo é um dos sólidos geométricos mais simples, sendo formado por seis faces quadradas idênticas. Para calcular a área total de um cubo, basta multiplicar a área de uma face por seis. A fórmula para calcular a área de uma face é:
A = L², em que A representa a área e L representa o comprimento de um lado do quadrado. Portanto, a área total de um cubo pode ser encontrada através da fórmula 6A = 6L².
Outro exemplo de sólido geométrico é a esfera, que é uma forma arredondada que não possui faces ou arestas. Para calcular a área de uma esfera, usa-se a fórmula:
4πr², em que r representa o raio da esfera e π é uma constante que representa a relação entre a circunferência de um círculo e seu diâmetro.
Um prisma retangular (paralelepípedo) é um sólido geométrico que possui duas faces idênticas e paralelas, chamadas de bases, conectadas por faces laterais. A área total de um prisma pode ser encontrada somando a área das duas bases com a área das faces laterais. Para calcular a área de uma face lateral de um prisma retangular, por exemplo, basta multiplicar o comprimento da base pela altura do prisma. A fórmula para calcular a área de uma base depende do formato do prisma.
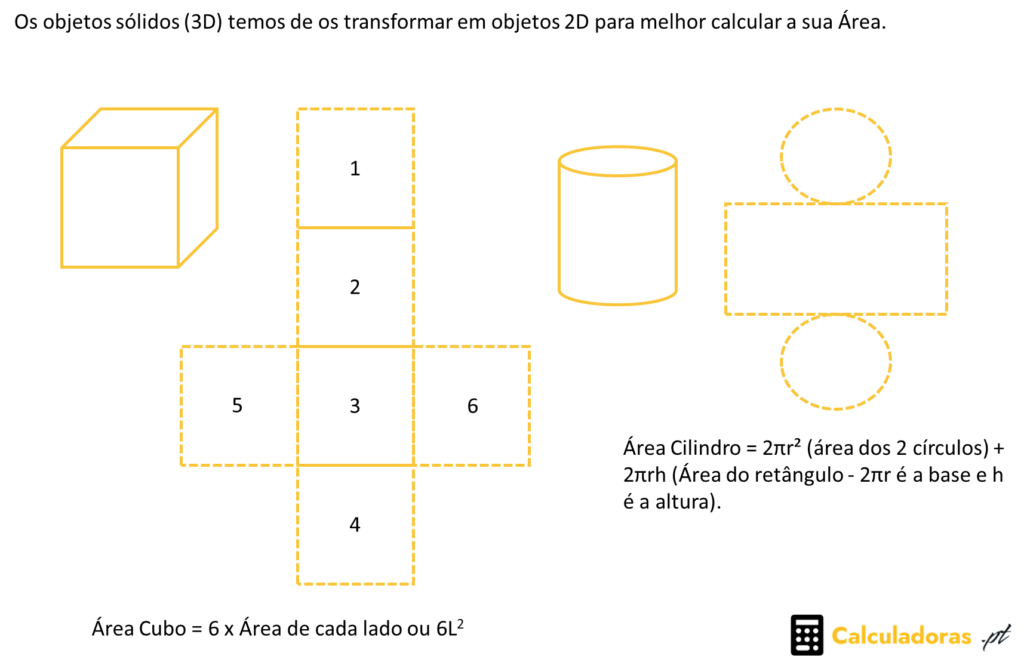
Já o cilindro é um sólido geométrico que possui duas bases circulares paralelas, conectadas por uma superfície lateral curva. Para calcular a área total de um cilindro, usa-se a fórmula:
2πr² + 2πrh, em que r representa o raio das bases e h representa a altura do cilindro.
Em suma, os sólidos geométricos são formas tridimensionais que ocupam espaço. A área de um sólido pode ser calculada a partir da soma das áreas de suas faces e superfícies laterais, utilizando fórmulas específicas para cada formato. Compreender as propriedades e fórmulas dos sólidos geométricos é essencial para diversas áreas, como arquitetura e engenharia.
Calcular a área do Círculo
Definições de Círculo e Circunferência
O círculo é uma figura geométrica que é definida como o conjunto de todos os pontos de um plano que estão a uma distância constante de um ponto central. Em outras palavras, é uma forma circular com um raio que se estende da borda até o centro.
Por outro lado, a circunferência é a curva que delimita a borda do círculo. É importante notar que a circunferência não é a mesma coisa que o círculo em si. A circunferência é uma linha curva fechada, enquanto o círculo é uma figura bidimensional.
Embora o círculo e a circunferência estejam intimamente relacionados, eles têm características e propriedades diferentes. Por exemplo, o círculo tem uma área definida, que é dada pela fórmula A = πr², onde “r” é o raio do círculo e “π” é a constante matemática Pi. Já a circunferência tem um comprimento definido, que é dado pela fórmula C = 2πr, onde “C” é o comprimento da circunferência.
Em suma, o círculo e a circunferência são duas formas geométricas fundamentais na matemática. O círculo é uma figura bidimensional que consiste em todos os pontos de um plano que estão a uma distância constante de um ponto central, enquanto a circunferência é a curva que delimita a borda do círculo. Espero que tenha ficado claro e informativo.

